XOR Problem in neural network

 

XOR problem with neural networks

The XOR gate can be usually termed as a combination of NOT and AND gates

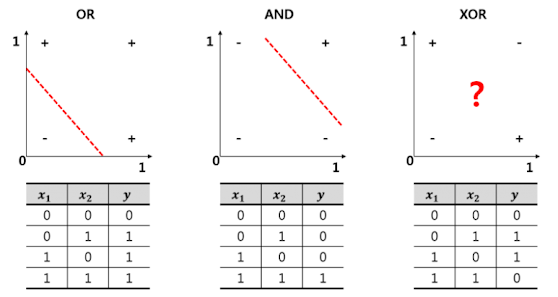
The linear separability of points

Linear separability of points is the ability to classify the data points in the hyperplane by avoiding the overlapping of the classes in the planes. Each of the classes should fall above or below the separating line and then they are termed as linearly separable data points. With respect to logical gates operations like AND or OR the outputs generated by this logic are linearly separable in the hyperplane

So here we can see that the pink dots and red triangle points in the plot do not overlap each other and the linear line is easily separating the two classes where the upper boundary of the plot can be considered as one classification and the below region can be considered as the other region of classification.

Need for linear separability in neural networks

Linear separability is required in neural networks is required as basic operations of neural networks would be in N-dimensional space and the data points of the neural networks 

Linear separability of data is also considered as one of the prerequisites which help in the easy interpretation of input spaces into points whether the network is positive and negative and linearly separate the data points in the hyperplane.

linear separable use cases and XOR is one of the logical operations which are not linearly separable as the data points will overlap the data points of the linear line or different classes occur on a single side of the linear line. 

we can see that above the linear separable line the red triangle is overlapping with the pink dot and linear separability of data points is not possible using the XOR logic. So this is where multiple neurons also termed as Multi-Layer Perceptron are used with a hidden layer to induce some bias while weight updating and yield linear separability of data points using the XOR logic. So now let us understand how to solve the XOR problem with neural networks.

Solution of xor problem

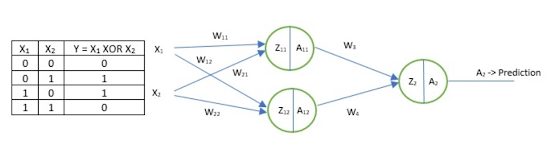
The XOR problem with neural networks can be solved by using Multi-Layer Perceptron’s or a neural network architecture with an input layer, hidden layer, and output layer.

 

To solve this problem, we add an extra layer to our vanilla perceptron, i.e., we create a Multi Layered Perceptron (or MLP). We call this extra layer as the Hidden layer. To build a perceptron, we first need to understand that the XOr gate can be written as a combination of AND gates, NOT gates and OR gates in the following way:

a XOr b = (a AND NOT b)OR(bAND NOTa)

 

 

So during the forward propagation through the neural networks, the weights get updated to the corresponding layers and the XOR logic gets executed. The Neural network architecture to solve the XOR problem will be as shown below.

 

 

 

problem wherein linear separability of data points is not possible using single neurons or perceptron’s. So for solving the XOR problem for neural networks it is necessary to use multiple neurons in the neural network architecture with certain weights and appropriate activation functions to solve the XOR problem with neural networks.

 

C Programming

 C Language 

C language Tutorial with programming approach for beginners and professionals, helps you to understand the C language tutorial easily. Our C tutorial explains each topic with programs.

The C Language is developed by Dennis Ritchie for creating system applications that directly interact with the hardware devices such as drivers, kernels, etc.

C programming is considered as the base for other programming languages, that is why it is known as mother language.